Monty Hall-problemet är baserat på en gammal TV-serie som hette Let’s Make a Deal. En deltagare i programmet blev visad tre stängda dörrar (numrerade 1, 2 och 3). Bakom varje dörr finns en belöning. En av belöningarna är dyrbar (traditionellt en bil) och de två andra är mindre dyrbara (traditionellt en get). Deltagaren får välja en dörr och får behålla den belöning som finns bakom dörren.
Nu till problemet. Deltagaren väljer en dörr men innan dörren öppnas så avbryter programledaren (Monty) och öppnar en av de dörrar som deltagaren inte valt och visar att det där bakom finns en get. Deltagaren får nu ett val innan den valda dörren öppnas; stå fast vid den valda dörren eller byta dörr. Hur maximerar deltagaren sin chans att vinna bilen?
Nu väljer vi ett tänkbart scenario som är generaliserbart och använder detta för att beräkna sannolikheter. I vårt scenario väljer deltagaren dörr 1. Monty öppnar då dörr 3 och visar att där bakom fanns en get. Vi utgår ifrån att Monty alltid öppnar en dörr bakom vilken det finns en get (och aldrig den dörr bakom vilken bilen finns). Först gör vi en tabell:
library(tibble)
monty_hall <- tibble(prior = rep(1/3, 3))Raderna i denna tabell representerar de tre olika hypoteserna att bilen är bakom dörr 1, 2 eller 3. De sannolikheter vi för in är sannolikheter för att bilen är bakom respektive dörr a priori, dvs. innan vi får ytterligare information. Med andra ord; utan ytterligare information så är sannolikheten att deltagaren valt rätt dörr 1/3. När Monty öppnar dörr tre så får vi ytterligare information och vi måste nu beakta sannolikheter under de tre olika hypoteserna:
- Om bilen är bakom dörr 1 så väljer Monty slumpmässigt mellan dörr 2 och 3. Sannolikheten att han öppnar dörr 3 är då
1/2. - Om bilen är bakom dörr 2 så måste Monty välja dörr 3. Sannolikheten att han öppnar dörr 3 under denna hypotes är
1. - Dörren kan inte vara bakom dörr 3 eftersom Monty öppnar den och visar en get. Sannolikheten för denna hypotes är
0.
Vi uppdaterar sannolikhetstabellen:
monty_hall[["likelihood"]] <- c(1/2, 1, 0) monty_hall # A tibble: 3 × 2 prior likelihood <dbl> <dbl> 1 0.333 0.5 2 0.333 1 3 0.333 0
Nu kan vi använda Bayes sats för att beräkna sannolikheter för att bilen är bakom de olika dörrarna:
monty_hall[["unnorm"]] <- monty_hall[["prior"]] * monty_hall[["likelihood"]]
monty_hall[["posterior"]] <- monty_hall[["unnorm"]] / sum(monty_hall[["unnorm"]])
monty_hall
# A tibble: 3 × 4
prior likelihood unnorm posterior
<dbl> <dbl> <dbl> <dbl>
1 0.333 0.5 0.167 0.333
2 0.333 1 0.333 0.667
3 0.333 0 0 0 Sannolikheten, a posteriori (med den nya informationen i beaktande), att bilen är bakom dörr 1 i det givna scenariot är 1/3 medan sannolikheten att bilen är bakom dörr 2 är 2/3. Deltagaren fördubblar sina chanser att vinna bilen om han/hon byter dörr. Detta scenario är generaliserbart och kan appliceras oavsett vilken dörr deltagaren väljer; om vi istället skulle utgå ifrån att deltagaren väljer dörr 2 och Monty öppnar dörr 1 så får vi:
monty_hall <- tibble(prior = rep(1/3, 3)) monty_hall[["likelihood"]] <- c(0, 1/2, 1) monty_hall[["unnorm"]] <- monty_hall[["prior"]] * monty_hall[["likelihood"]] monty_hall[["posterior"]] <- monty_hall[["unnorm"]] / sum(monty_hall[["unnorm"]]) monty_hall # A tibble: 3 × 4 prior likelihood unnorm posterior <dbl> <dbl> <dbl> <dbl> 1 0.333 0 0 0 2 0.333 0.5 0.167 0.333 3 0.333 1 0.333 0.667
Med andra ord; sannolikheten att vinna bilen fördubblas om man byter dörr (oavsett vilken dörr man valde och vilken dörr Monty öppnar).
Nedan har jag skrivit två funktioner för att lösa liknande uppgifter i R:
bt <- function(event, prior, likelihood) {
require(tibble)
bt <- tibble('event' = event,
'prior' = prior,
'likelihood' = likelihood)
bt[, 'unnorm'] <- bt[, 'prior'] * bt[, 'likelihood']
bt[, 'posterior'] <- bt[, 'unnorm'] / sum(bt[, 'unnorm'])
return(bt)
}
update_bt <- function(bt, n_likelihood) {
event <- bt[['event']]
prior <- bt[['posterior']]
n_unnorm <- prior * n_likelihood
n_posterior <- n_unnorm / sum(n_unnorm)
require(tibble)
return(tibble('event' = event,
'prior' = prior,
'likelihood' = n_likelihood,
'unnorm' = n_unnorm,
'posterior' = n_posterior))
}
Funktionen bt() tar tre argument; event som är de möjliga utfallen, prior som är sannolikheten a priori för respektive utfall och likelihood som är sannolikhet för utfallen med ny data. Funktionen update_bt() utför ytterligare en uppdatering av data och tar en tabell från första funktionen som första argument och en vektor av nya sannolikheter som andra argument.
Monty Hall-problemet kan då, så som beskrivet enligt ovan, lösas enligt:
monty_hall <- bt(1:3, 1/3, c(1/2, 1, 0)) monty_hall # A tibble: 3 × 5 event prior likelihood unnorm posterior <int> <dbl> <dbl> <dbl> <dbl> 1 1 0.333 0.5 0.167 0.333 2 2 0.333 1 0.333 0.667 3 3 0.333 0 0 0
Kakproblemet
Vi har 101 skålar med kakor som är antingen vanilj eller choklad. I skål 1 finns 0% vaniljkakor, i skål 2 finns 1% vanlijkakor, i skål 3 finns 2% vaniljkakor osv. upp till skål 101 i vilken det finns 100% vaniljkakor.
Vi har nu valt en slumpmässig kaka som visar sig vara vanilj. Från vilken skål kom den mest sannolikt?
kakproblemet <- bt(event = 0:100,
prior = (101 / 100) - 1,
likelihood = 0:100 / 100)
which.max(kakproblemet[['posterior']])
# [1] 101
Här är (självklart) skål 101 mest sannolik eftersom den innehåller 100% vaniljkakor. Nu lägger vi tillbaka kakan och drar ytterligare en slumpmässig kaka från samma skål. Även denna gång blir det vanilj.
kakproblemet <- update_bt(kakproblemet,
n_likelihood = 0:100 / 100)
which.max(kakproblemet[['posterior']])
# [1] 101
Även efter denna nya information är skål 101 (självklart) mest sannolik. Men vi gör samma sak en gång till och drar nu en chokladkaka. Vi har dragit vanilj, vanilj, choklad. Vilken är den mest sannolika skålen?
kakproblemet <- update_bt(kakproblemet,
n_likelihood = 1 - (0:100 / 100))
which.max(kakproblemet[['posterior']])
# [1] 68
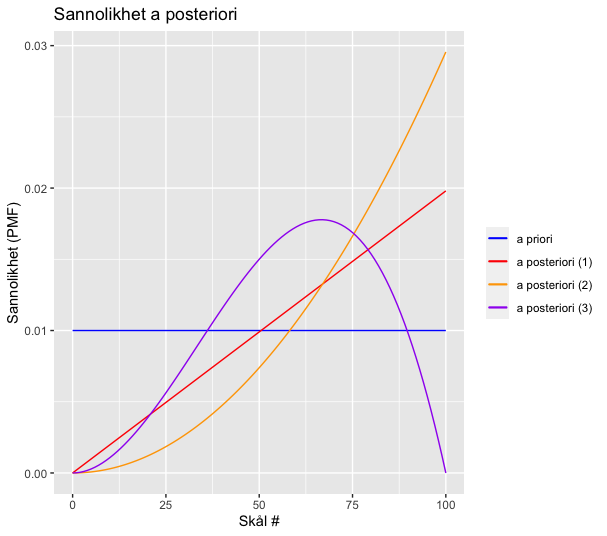
Den mest sannolika skålen är skål 68. Vi kan också åskådliggöra täthetsfunktionen efter de olika dragningarna:
posteriors <- tibble(
event = kakproblemet_1[['event']],
prior = kakproblemet_1[['prior']],
posterior_1 = kakproblemet_1[['posterior']],
posterior_2 = kakproblemet_2[['posterior']],
posterior_3 = kakproblemet_3[['posterior']]
)
library(ggplot2)
ggplot(posteriors, aes(x = event)) +
geom_line(aes(y = prior, color = "a priori")) +
geom_line(aes(y = posterior_1, color = "a posteriori (1)")) +
geom_line(aes(y = posterior_2, color = "a posteriori (2)")) +
geom_line(aes(y = posterior_3, color = "a posteriori (3)")) +
xlab("Skål #") +
ylab("Sannolikhet (PMF)") +
scale_colour_manual("", breaks = c("a priori", "a posteriori (1)", "a posteriori (2)", "a posteriori (3)"), values = c("blue", "red", "orange", "purple")) +
labs(title="Sannolikhet a posteriori")
Elvis Presleys tvillingbror
Elvis Presley hade en tvillingbror som dog vid födseln. Vad är sannolikheten att de var enäggstvillingar? 1935 var ungefär 1/3 av alla tvillingar som föddes enäggstvillingar.
Här tänker vi oss två olika händelser: de var enäggstvillingar eller de var inte enäggstvillingar. Om de var enäggstvillingar så är det 100% sannolikhet att tvillingen var en bror. Om de inte var enäggstvillingar så är det 50% sannolikhet att tvillingen var en bror.
elvis <- bt(c('Enäggs', 'Tvåäggs'), c(1/3, 2/3), c(1, 1/2))
elvis
# A tibble: 2 × 5
event prior likelihood unnorm posterior
<chr> <dbl> <dbl> <dbl> <dbl>
1 Enäggs 0.333 1 0.333 0.5
2 Tvåäggs 0.667 0.5 0.333 0.5Det är 50% sannolikhet att det var en enäggstvilling.
Lämna ett svar