Vid regressionsanalys tar vi fram ett matematiskt förhållande mellan två variabler. Ibland är regressionsanalys inte tillämpbart alls av olika anledningar. Ibland kan valet av regressionsmetod spela roll för hur bra det matematiska sambandet avspeglar det verkliga förhållandet mellan variablerna.
Nedan följer tre exempel på hur regression kan utföras. Dessa exempel är valda för sin tillämpbarhet inom laboratoriemedicin.
Data
Vi börjar med att skapa heteroskedastisk data (data med heterogen varians) som simulerar resultat från två immunkemiska analyser.
library(tibble)
set.seed(13)
x <- runif(100, 0, 100)
data <- tibble(x = x, y = 1.10 * x - 0.001 * x^2 + rnorm(100, 0, 1) * (2 + 0.05 * x) + 15)För att få en uppfattning om denna data gör vi först ett enkelt spridningsdiagram
library(ggplot2)
g1 <- data |> ggplot(aes(x, y)) +
geom_point() +
labs(title = "Regression",
subtitle = "Jämförelse av olika regressionsmodeller",
x = "Befintlig metod",
y = "Ny metod")
g1
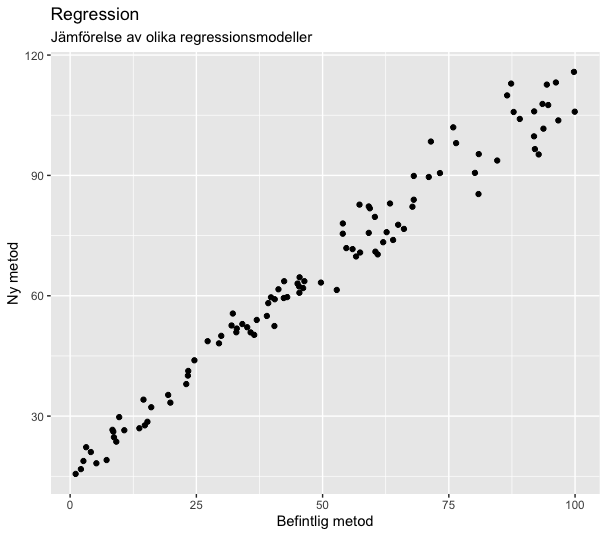
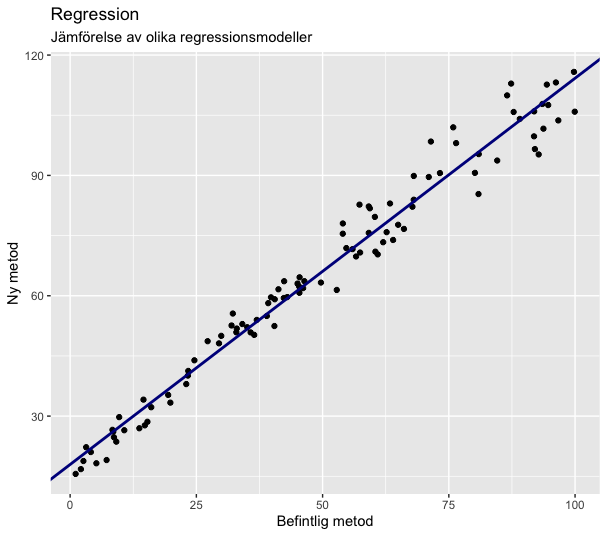
Minsta-kvadratmetoden (OLS)
Minsta-kvadratmetoden, eller ordinary least squares (OLS) på engelska, är en regressionsmetod där summan av alla residualer i kvadrat minimeras. Här definieras en residual som det vertikala avståndet från en datapunkt till regressionslinjen. Regressionslinjen väljs så att summan av alla residualer i kvadrat minimeras.
Vid minsta-kvadratmetoden görs antagandet att det inte finns något mätfel i den befintliga metoden (x-axelvärdet) och att det datan är heteroskedastisk (att spridningen av y-axelvärdet är konstant). Inget av dessa är uppfyllt vid jämförelse av bioanalytiska metodjämförelser.
Regression med minsta kvadratmetoden kan utföras i Rs baspaket men här används funktionen mcreg() från paketet mcr.
library(mcr)
ols <- mcreg(data[["x"]],
data[["y"]],
method.reg = "LinReg")
g1 + geom_abline(slope = ols@para[2],
intercept = ols@para[1],
color = "darkblue",
size = 1)
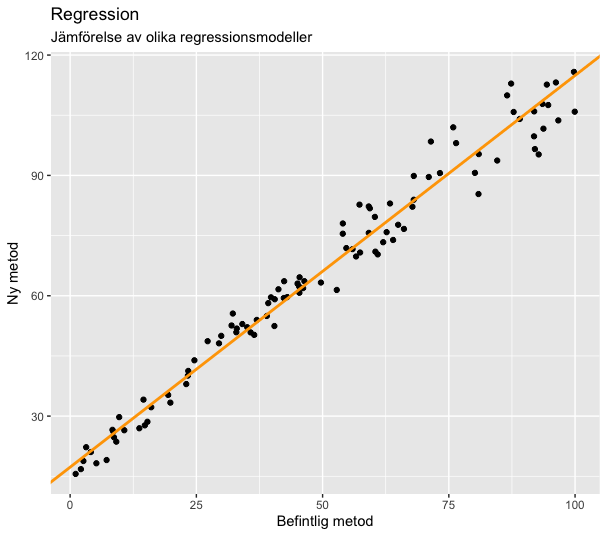
Deming-regression
Skillnaden mellan Deming och minsta kvadratmetoden är att Deming inte gör antagandet att den befintliga metoden är felfri. Här definieras en residual som det vinkelräta avståndet mellan en datapunkt och dess motsvarande värde på regressionslinjen.
deming <- mcreg(data[["x"]],
data[["y"]],
method.reg = "Deming")
g1 + geom_abline(slope = deming@para[2],
intercept = deming@para[1],
color = "orange",
size = 1)
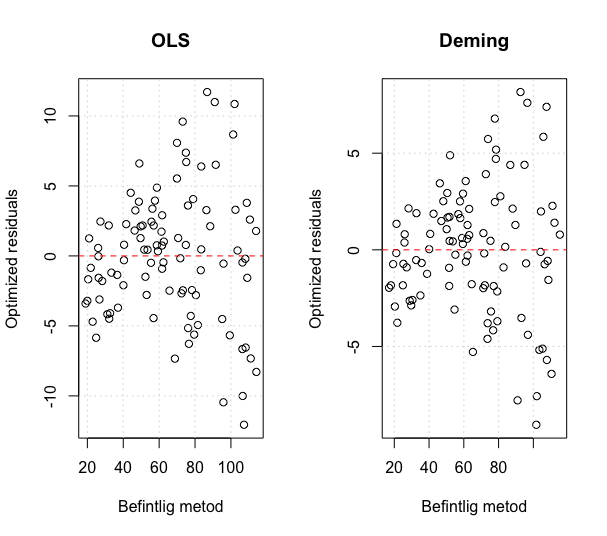
Vi kan visualisera residualerna och se att det finns en liten skillnad mellan metoderna med funktionen plotResiduals() från mcr.
par(mfrow = c(1, 2)) plotResiduals(ols, main = "OLS", xlab = "Befintlig metod") plotResiduals(deming, main = "Deming", xlab = "Befintlig metod")
Om vi har kartlagt imprecision för de två metoderna och denna skiljer sig (mätosäkerheten är olika för de två instrumenten), så kan vi använda kvoten av metodernas varians som argument i mcreg() för att få en bättre regressionsmodell.
mcreg(data[["x"]],
data[["y"]],
method.reg = "Deming")@para
mcreg(data[["x"]],
data[["y"]],
method.reg = "Deming",
error.ratio = 1.2)@para# EST SE LCI UCI # Intercept 17.269330 NA 15.8986463 18.775187 # Slope 0.976428 NA 0.9425787 1.014507 # EST SE LCI UCI # Intercept 17.2058655 NA 15.8996476 18.520266 # Slope 0.9777108 NA 0.9444235 1.012362
Viktning
Om vår data är heteroskedastisk kan vi vikta regressionen. Detta är en matematisk justering vilket ger mer vikt åt datapunkter i områden med mindre spridning (datapunkter i områden med hög spridning anses då mer osäkra och påverkar regressionslinjens lutning mindre).
deming_v <- mcreg(data[["x"]],
data[["y"]],
method.reg = "WDeming")
g1 +
geom_abline(slope = deming@para[2],
intercept = deming@para[1],
color = "orange",
size = 1) +
geom_abline(slope = deming_v@para[2],
intercept = deming_v@para[1],
color = "darkgreen",
size = 1)
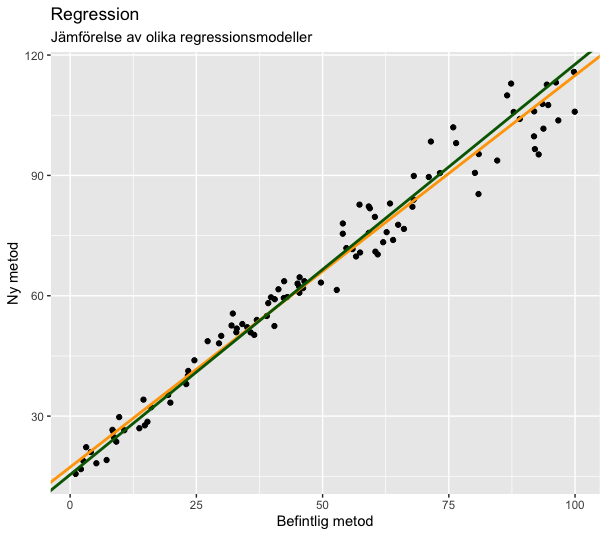
Passing-Bablok
Passing-Bablok skiljer sig från de ovanstående regressionsmetoderna på så sätt att det inte går ut på att minimera summan av residualer. Istället beräknas lutning för alla tänkbara kombinationer av datapunkter. Justeringar görs för punkter som genererar oändligt stora eller små lutningar. Man kan inte vikta en Passning-Bablok eftersom det inte finns några residualer att applicera vikt på.
Av alla de regressionslinjer som genereras väljs medianen ut.
pb <- mcreg(data[["x"]],
data[["y"]],
method.reg = "PaBa")
g1 + geom_abline(slope = pb@para[2],
intercept = pb@para[1],
color = "pink",
size = 1)
Eftersom Passing-Bablok är rangbaserad påverkas den slutgiltiga lutningen endast lite av outliers och extremvärden.
Ovanstående grafer har genererats med ggplot2. Som alternativ innehåller mcr funktioner för att skapa snygga grafer.
par(mfrow = c(1, 1))
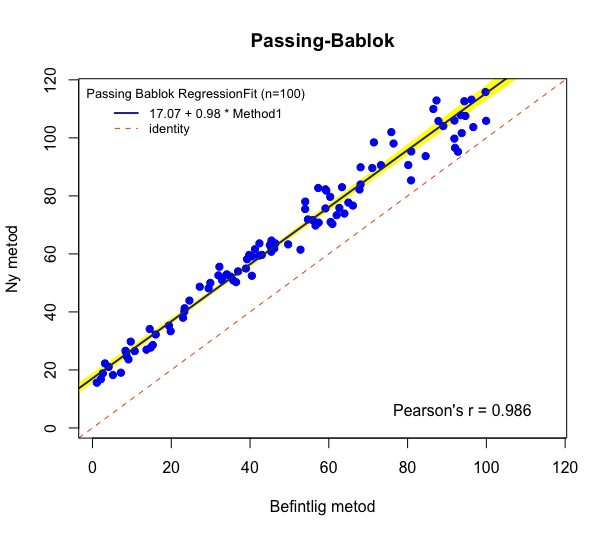
MCResult.plot(pb,
equal.axis = TRUE,
x.lab = "Befintlig metod",
y.lab = "Ny metod",
points.col = "#0000F0",
points.pch = 19,
ci.area = TRUE,
ci.area.col = "#FFFF00",
main = "Passing-Bablok",
sub = "",
add.grid = FALSE,
points.cex = 1)
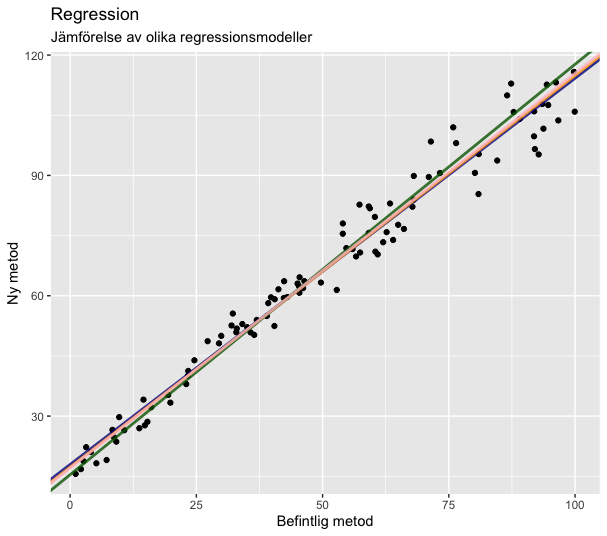
OLS, Deming, viktad Deming och Passing-Bablok i samma graf för jämförelse
Lämna ett svar